Variance

Dr. Mine Dogucu

1 / 24

If there was no variance there would be no statistics.

2 / 24

What if?We want to understand average number of sleep Irvine residents get.  What if everyone in Irvine slept 8 hours every night? (sleep = {8, 8,..., 8})
3 / 24

What if?

We want to understand average number of sleep Irvine residents get. What if everyone in Irvine slept 8 hours every night? (sleep = {8, 8,..., 8})
We want to predict who will graduate college. What if everyone graduated college? (graduate = {TRUE, TRUE,..., TRUE})

4 / 24

What if?

We want to understand average number of sleep Irvine residents get. What if everyone in Irvine slept 8 hours every night? (sleep = {8, 8,..., 8})
We want to predict who will graduate college. What if everyone graduated college? (graduate = {TRUE, TRUE,..., TRUE})
We want to understand if Android users spend more time on their phones when compared to iOS users. What if everyone spent 3 hours per day on their phones? (time = {3, 3,..., 3}, os = {Android, Android, .... iOS})

5 / 24

What if?

We want to understand average number of sleep Irvine residents get. What if everyone in Irvine slept 8 hours every night? (sleep = {8, 8,..., 8})
We want to predict who will graduate college. What if everyone graduated college? (graduate = {TRUE, TRUE,..., TRUE})
We want to understand if Android users spend more time on their phones when compared to iOS users. What if everyone spent 3 hours per day on their phones? (time = {3, 3,..., 3}, os = {Android, Android, .... iOS})
We want to understand, if birth height and weight are positively associated in babies. What if every baby was 7.5 lbs? (weight = {7.5, 7.5,..., 7.5}, height = {20, 22,..., 18})

6 / 24

In all this fake scenarios there would be no variance in sleep, graduate, time, weight. These variables would all be constants thus would not even be a variable.

7 / 24

Things vary. We use statistics to understand how things vary and often we want to know why they vary.

8 / 24

Consider Dr. Dogucu teaching three classes. All of these classes have 5 students. Below are midterm results from these classes. Which of the classes have a higher variance?

Class 1: 80 80 80 80 80
Class 2: 76 78 80 82 84
Class 3: 60 70 80 90 100

9 / 24

Consider Dr. Dogucu teaching three classes. All of these classes have 5 students. Below are midterm results from these classes. Which of the classes have a higher variance?

Class 1: 80 80 80 80 80
Class 2: 76 78 80 82 84
Class 3: 60 70 80 90 100

All of these classes have a mean of 80 points. But the data differ! In order to explain how these are different we examine how far off each observed value is from the mean on "average". In class 1 all students are at the mean value so there is no variance. Class 2 students deviate from the mean slightly on "average". Class 3 has the highest deviation from the mean on "average".

10 / 24

Calculating the Variance

11 / 24

The Mean

Consider the following data which represents the number of hours slept for 10 people who were surveyed.

$y_{i} = {7, 7.5, 8, 5.5, 10, 7.2, 7, 8, 9, 8}$

y_i <- c(7, 7.5, 8, 5.5, 10, 7.2, 7, 8, 9, 8)

12 / 24

The Mean

Consider the following data which represents the number of hours slept for 10 people who were surveyed.

$y_{i} = {7, 7.5, 8, 5.5, 10, 7.2, 7, 8, 9, 8}$

y_i <- c(7, 7.5, 8, 5.5, 10, 7.2, 7, 8, 9, 8)

mean(y_i)

## [1] 7.72

$\bar{y} = 7.72 hr$

13 / 24

Sample Size

length(y_i)

## [1] 10

$n = 10$

14 / 24

Sample Size

length(y_i)

## [1] 10

$n = 10$

$i = {1, 2, . . . n}$

15 / 24

Sample Size

length(y_i)

## [1] 10

$n = 10$

$i = {1, 2, . . . n}$

$i = {1, 2, . . . 10}$

16 / 24

Standard Deviation

sd(y_i)

## [1] 1.218195

$s = 1.218195 hr$

Variance

var(y_i)

## [1] 1.484

$s^{2} = 1.484 {hr}^{2}$

17 / 24

$n = 10$ , $\bar{y} = 7.72 hr$ , $s = 1.218195 hr$

Among 10 people the average number of sleep was 7.72 hours. However, everybody did not sleep 7.72 hours. There was deviation from the mean. The standard deviation from the mean was 1.218195 hours. The variance is the squared standard deviation which was $1.484 {hr}^{2}$ .

18 / 24

How did R calculate the variance?

19 / 24

Standard deviation and Variance
yi    yi - ȳ   (yi - ȳ) 2

5   5.5-7.72 = -2.22 hr  (-2.2 hr)2 = 4.9284 hr 2 
 
 7-7.72 = -0.72 hr  (-0.72 hr)2 = 0.5184 hr 2
 
 7-7.72 = -0.72 hr  (-0.72 hr)2 = 0.5184 hr 2
 
2   7.2-7.72 = -0.52 hr  (-0.52 hr)2 = 0.2704 hr 2
 
5   7.5-7.72 = -0.22 hr  (-0.22 hr)2 = 0.0484 hr 2
 
 8-7.72 = 0.28 hr  (0.28 hr)2 = 0.0784 hr 2
 
  8-7.72 = 0.28 hr  (0.28 hr)2 = 0.0784 hr 2
 
 8-7.72 = 0.28 hr  (0.28 hr)2 = 0.0784 hr 2
 
 9-7.72 = 1.28 hr  (1.28 hr)2 = 1.6384 hr 2
 
 10-7.72 = 2.28 hr  (2.28 hr)2 = 5.1984 hr 2
/ 24

y_i	y_i - ȳ	(y_i - ȳ) ²
5.5	5.5-7.72 = -2.22 hr	(-2.2 hr)² = 4.9284 hr ²
7	7-7.72 = -0.72 hr	(-0.72 hr)² = 0.5184 hr ²
7	7-7.72 = -0.72 hr	(-0.72 hr)² = 0.5184 hr ²
7.2	7.2-7.72 = -0.52 hr	(-0.52 hr)² = 0.2704 hr ²
7.5	7.5-7.72 = -0.22 hr	(-0.22 hr)² = 0.0484 hr ²
8	8-7.72 = 0.28 hr	(0.28 hr)² = 0.0784 hr ²
8	8-7.72 = 0.28 hr	(0.28 hr)² = 0.0784 hr ²
8	8-7.72 = 0.28 hr	(0.28 hr)² = 0.0784 hr ²
9	9-7.72 = 1.28 hr	(1.28 hr)² = 1.6384 hr ²
10	10-7.72 = 2.28 hr	(2.28 hr)² = 5.1984 hr ²

Total distance from the mean

$Σ_{i = 1}^{n} (y_{i} - \bar{y})^{2} =$

$4.9284 + 0.5184 + 0.5184 + 0.2704 + 0.0484 +$ $0.0784 + 0.0784 + 0.0784 + 1.6384 + 5.1984 = 13.356 {hr}^{2}$

21 / 24

Sample variance

$s^{2} = \frac{Σ_{i = 1}^{n} (y_{i} - \bar{y})^{2}}{n - 1}$

$s^{2} = \frac{13.356}{10 - 1} = 1.484 {hr}^{2}$

22 / 24

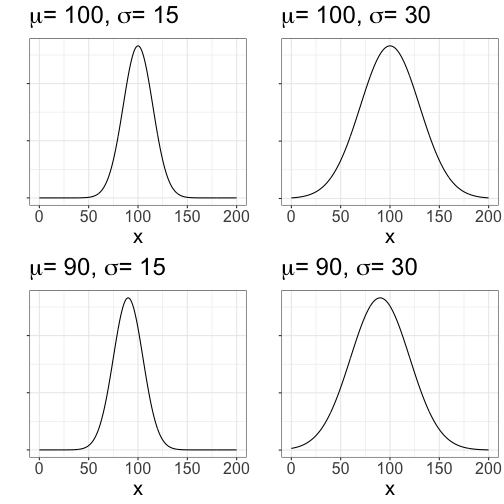
Notation

	Sample Statistic	Population Parameter
Mean	ȳ	μ
Standard Deviation	s	σ
Variance	s²	σ²

Sample size is denoted by $n$ .

23 / 24

24 / 24

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help