Data

lapd <- lapd %>% 
  janitor::clean_names() %>% 
  filter(year == 2018) %>% 
  select(base_pay)

We will be using payroll data from Los Angeles Police Department (LAPD) from 2018.

glimpse(lapd)

## Rows: 14,824
## Columns: 1
## $ base_pay <dbl> 119321.60, 113270.70, 148116.00, 78676.87, 109373.63, 95001.…

Population Distribution

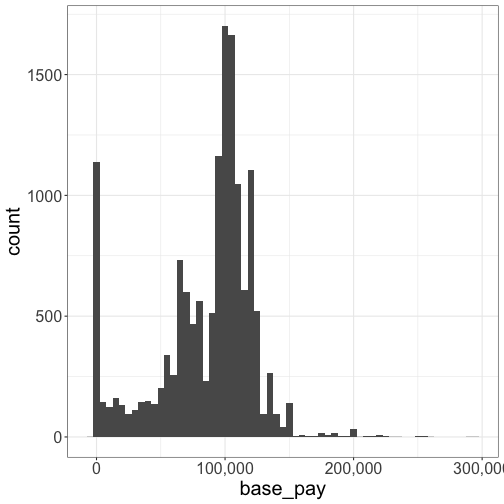
True Median

median(lapd$base_pay)

## [1] 97600.66

This is a population parameter. We often do not know population parameters but we can estimate them. Estimation requires some sample data.

Sample 1

##  [1]      0.00 101248.80 109378.40 132957.60  90956.57 132743.97 104091.10
##  [8] 104100.80  48696.00 125958.40

Median of sample 1 is 104095.95.

Sample 2

##  [1] 95971.20 96193.81     0.00 34479.44 90005.56 66881.94 75342.80 68034.18
##  [9] 54612.80     0.00

Median of sample 2 is 67458.06.

Sample 3

##  [1] 143967.89 109386.56 119321.60 106724.41  65343.46  90583.56  96848.28
##  [8] 103892.80  67380.10  85136.00

Median of sample 3 is 100370.54.

Sample 4

##  [1]      0.00 101248.80 109378.40 132957.60  90956.57 132743.97 104091.10
##  [8] 104100.80  48696.00 125958.40

Median of sample 4 is 104095.95.

Sampling Variability

• Note that the median varies from sample to sample. Each sample's median is not necessarily the population median we are trying to estimate. There is variance of sample medians.

• In real life taking samples from the population is costly. We often have only have one sample that we can use to estimate the population parameter.

• How can we take sampling variability into account when we only have one sample?

  • There are different ways to do this. We will use bootstrapping in this class.
  • If you want to learn more on estimating population parameters using sample data, I encourage you to take a statistics classes.

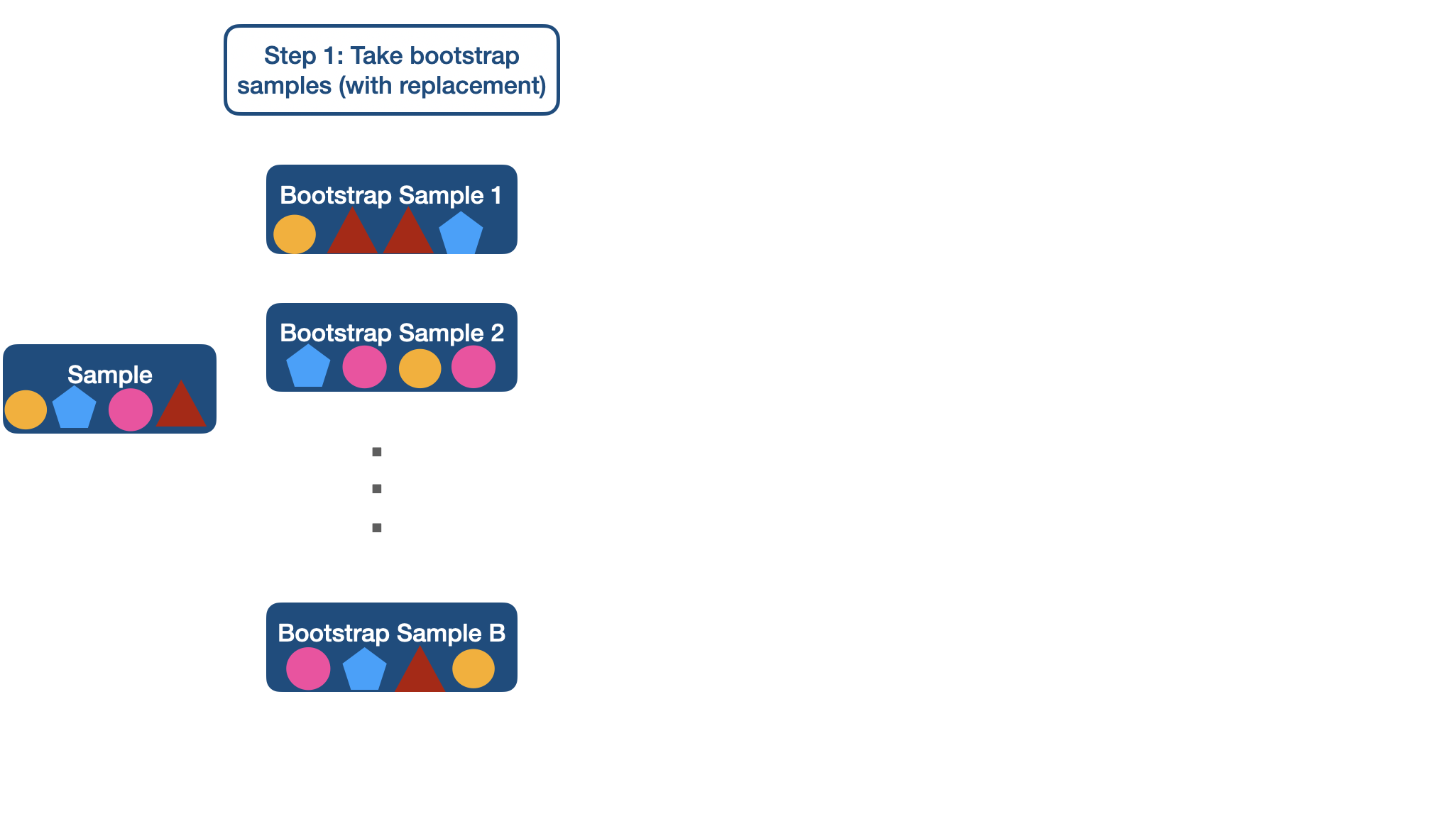
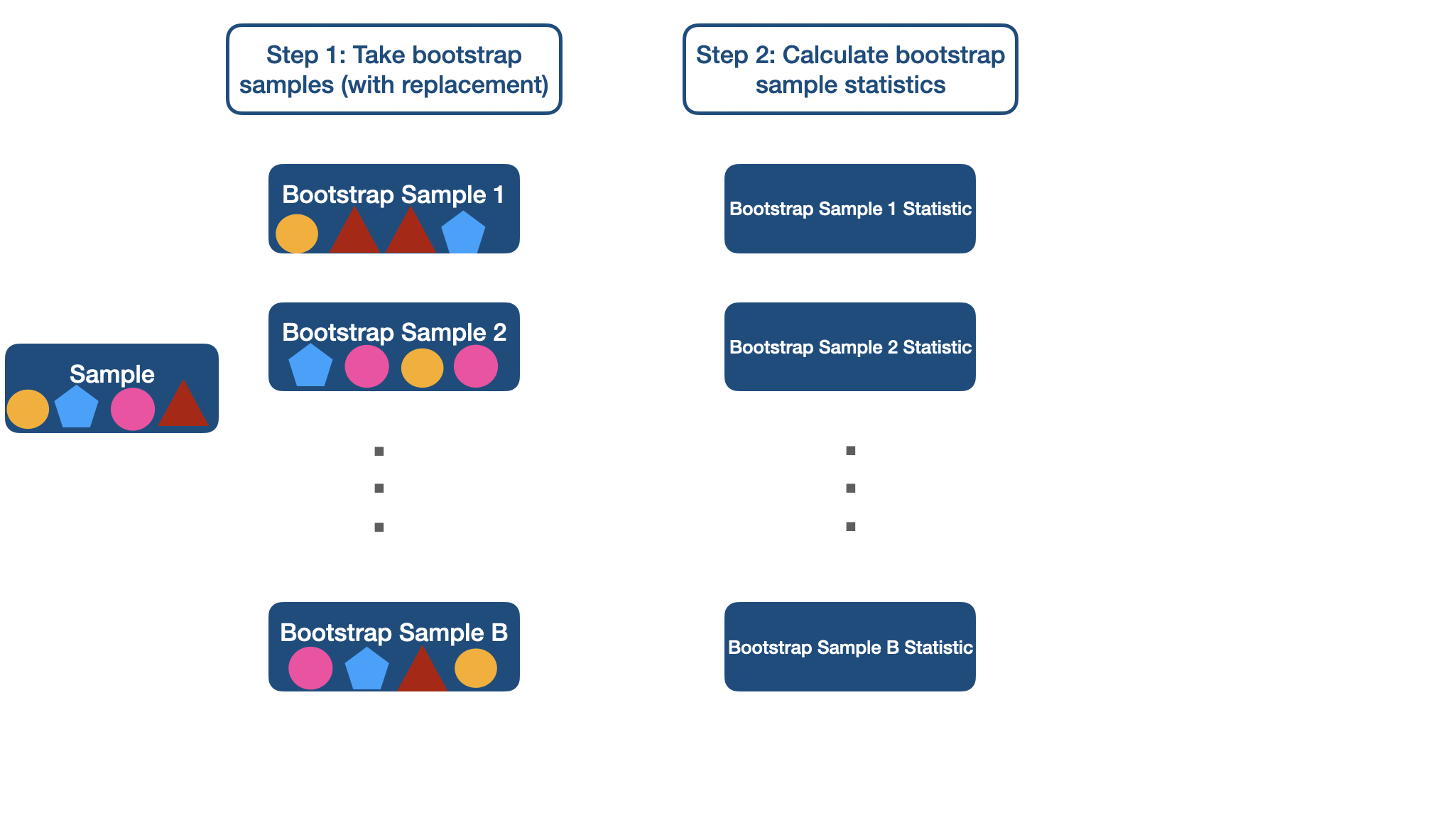
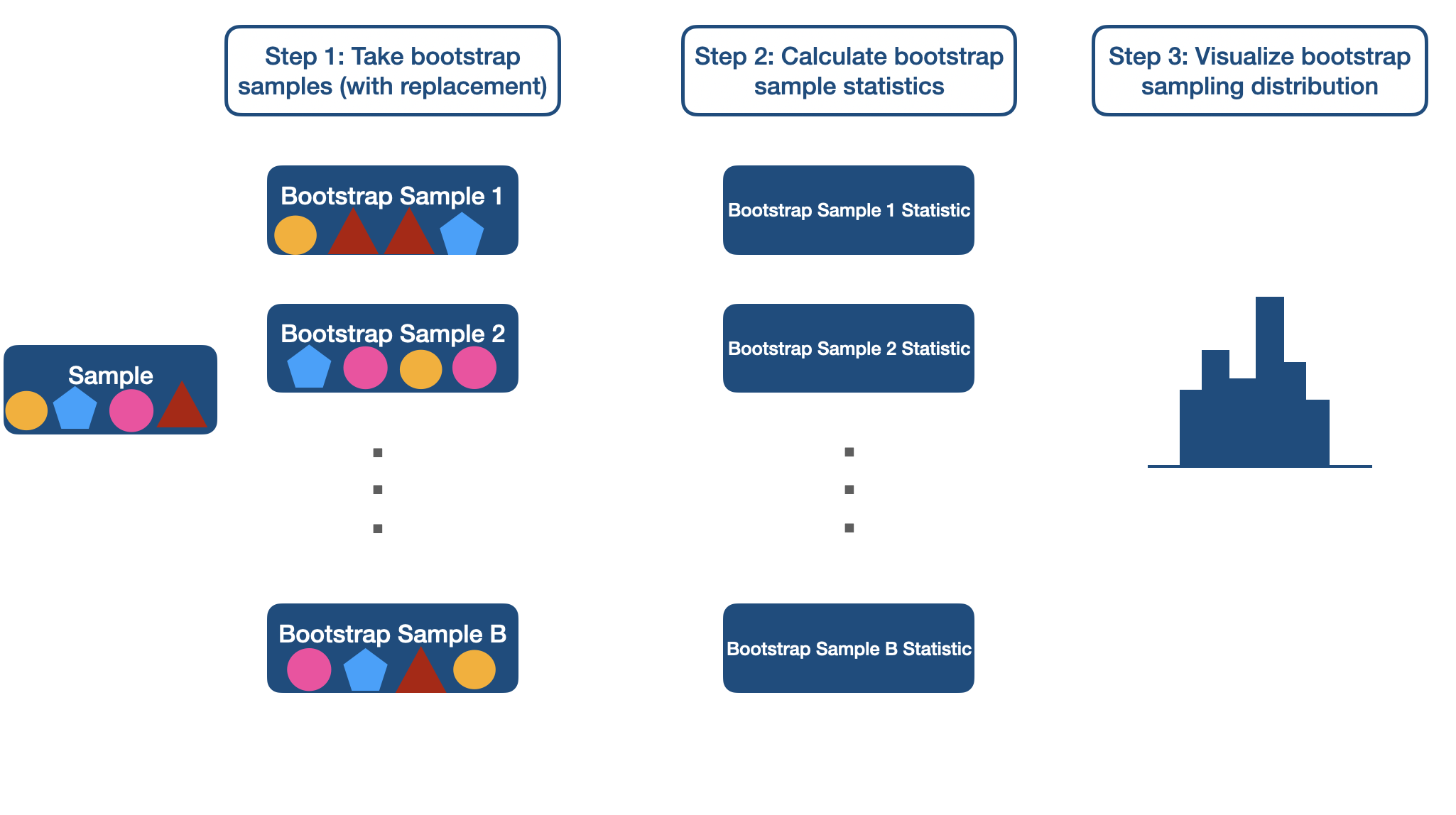
Random Sample ( $n$ = 50)

library(infer) # for bootstrap related functions
set.seed(12345)
lapd_sample <- sample_n(lapd, 20)
lapd_sample$base_pay

##  [1]      0.00 101248.80 109378.40 132957.60  90956.57 132743.97 104091.10
##  [8] 104100.80  48696.00 125958.40  95971.20  96193.81      0.00  34479.44
## [15]  90005.56  66881.94  75342.80  68034.18  54612.80      0.00

Bootstrapping

boot <- lapd_sample %>% 
  specify(response = base_pay) %>% 
  generate(reps = 1000, type = "bootstrap") %>% 
  calculate(stat = "median")

visualize(boot) +
  scale_x_continuous(labels = scales::comma_format()) +
  theme_bw() +
  theme(text = element_text(size = 20))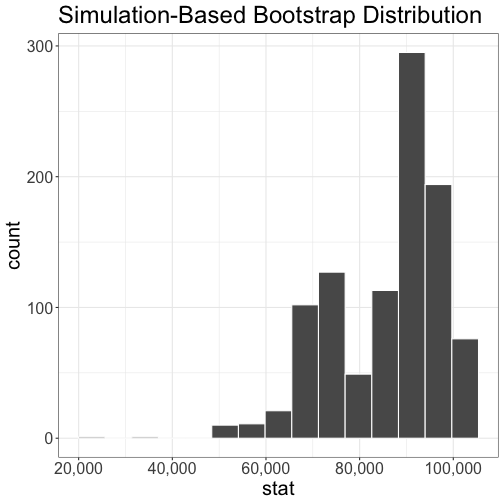

95% Confidence Interval

We can construct the 95% confidence interval by calculating the 2.5th and 97.5th percentiles of the bootstrap distribution.

boot %>% 
  summarize(lower_bound = quantile(stat, 0.025),
            upper_bound = quantile(stat, 0.975))

## # A tibble: 1 x 2
##   lower_bound upper_bound
##         <dbl>       <dbl>
## 1      60747.     104091.

This confidence interval captures the true median (97600.66).

Commonly used confidence levels in practice are 90% (blue), 95% (red), and 99 (black)%

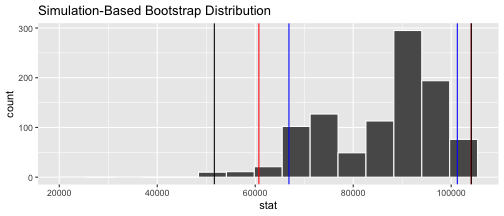
Interpretation of Confidence Intervals

Calculating a confidence interval does not guarantee that we will capture the true value of population parameter in the interval.

If we were to take considerable large number of samples (we only had one sample) and construct 95% confidence intervals for each of the samples we would expect about 95% of the confidence intervals to capture the the true value of population parameter in the interval.

Take-Away Messages

• Sample statistics $\ne$ population parameter.

• Different samples can have different statistics, thus there is sampling variability.

• We have constructed a confidence interval to infer about a median but we could do this for mean, proportion, difference between two group means etc.

• More on constructing confidence intervals (and hypothesis testing) in other statistics classes. In this class, we will focus on using and interpreting confidence intervals. R will do the calculations for us.